Question

AA, BBB, and CCC are collinear, and BBB is between AAA and CCC. The ratio of ABABA, B to ACACA, C is 3:43:43, colon, 4. If AAA is at (-8,1)(−8,1)(, minus, 8, comma, 1, )and BBB is at (-2,-2)(−2,−2)(, minus, 2, comma, minus, 2, ), what are the coordinates of point CCC?

Answer 1

The coordinates of point C are (0,-3).

Explanation:

It is given that A, B, and C are collinear and B is between A and C.

The ratio of AB to AC is 3:4. Let length of AB and AC be 3x and 4x respectively.

`AC=AB+BC`

`4x=3x+BC`

`x=BC`

`(AB)/(BC)=(3x)/(x)=3:1`.

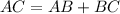
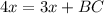
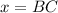
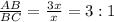Therefore, AB to BC is 3:1.

The given ordered pairs are A(-8,1) and B(-2,-2).

Let as assume that the coordinate of C is (a,b).

Section formula:

If a point divides a line segment in m:n whose end points are
`(x_1,y_1)` and
`(x_2,y_2)`, then the coordinates of that point are

`((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))`

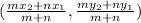
Point B divided the line AC is 3:1. Using section formula we get

`B=(((3)(a)+(1)(-8))/(3+1),((3)(b)+(1)(1))/((3)+(1)))`

`B=((3a-8)/(4),(3b+1)/(4))`

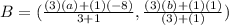
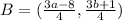
The coordinates of B are (-2,-2).

`(-2,-2)=((3a-8)/(4),(3b+1)/(4))`

On comparing both sides.

`-2=(3a-8)/(4)`

`-8=3a-8`

`0=3a`

`a=0`

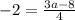
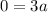
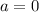
The value of a is 0.

`-2=(3b+1)/(4)`

`-8=3b+1`

`-9=3b`

`-3=b`

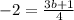
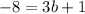
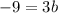
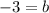
The value of b is -3.

Therefore the coordinates of point C are (0,-3).