Question

Please explain how to do this

Answer 1

Sure. I don't know what a drawing pin is, but I suppose that doesn't matter.

The mean is another word for the average. She has 10 boxes, so we're essentially adding up 10 numbers of pins and dividing the result by 10.

If we were to write it out, we'd get

`\bar{x} = \frac {1}{10} (29 + 29 +30+30+30+30+30+31+31+32)`

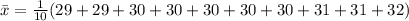
There's no reason to write out the repeated additions; they're just multiplications by the frequency. So the calculation of the mean can be compacted a bit into what's called a weighted average:

`\bar{x} = \frac {1}{2+5+2+1} (2 * 29 + 5 * 30+ 2 * 31 + 1 * 32)`

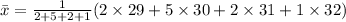
Working it out

`\bar{x} = \frac {1}{10} (302) = 30.2`

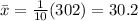
Answer: 30.2