Question

Write the equation of the line that passes through the given points (0,1) (-7,-5)

Answer 1

Explanation:

Answer 2

The line equation that passes through the given points (0,1) (-7,-5) is 6x – 7y + 7 = 0.

SOLUTION:

Given, two points are A(0, 1) and B(-7, -5).

We need to find the line equation that passes through the given two points.

We know that, general equation of a line passing through two points
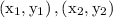`$\left(\mathrm{x}_(1), \mathrm{y}_(1)\right),\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)$` is given by

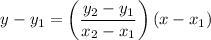`$y-y_(1)=\left((y_(2)-y_(1))/(x_(2)-x_(1))\right)\left(x-x_(1)\right)$` --- 1

Here,in our problem
`\mathrm{x}_(1)=0, \mathrm{y}_(1)=1, \mathrm{x}_(2)=-7$ and $\mathrm{y}_(2)=-5$`

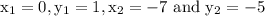
Now substitute the values in (1)

`$y-1=\left((-5-1)/(-7-0)\right)(x-0)$`

`$y-1=(-6)/(-7)(x)$`

`$y-1=(6)/(7) x$`

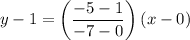
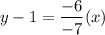
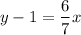
7y – 7 = 6x

6x – 7y + 7 = 0

Hence, the line equation that passes through the given points is 6x – 7y + 7 = 0.