1)
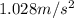
We can solve this part by using Newton's second law:
 (1)
(1)
where
F is the net force
m is the mass
a is the acceleration
There are two forces acting on the boat:
 forward
forward
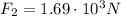 backward
backward
So the net force is
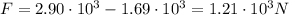
We know that the mass of the boat is
m = 1177.5 kg
So we can now use eq.(1) to find the acceleration:
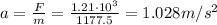
2) 161.0 m
We can solve this part by using the following suvat equation:

where
s is the distance travelled
u is the initial velocity
t is the time
a is the acceleration
Here we have
u = 0 (the boat starts from rest)
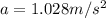
Substituting t = 17.7 s, we find the distance covered:
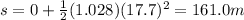
3) 18.2 m/s
The speed of the boat can be found with the following suvat equation

where
v is the final velocity
u is the initial velocity
t is the time
a is the acceleration
In this case we have
u = 0 (the boat starts from rest)
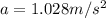
And substituting t = 17.7 s, we find the final velocity:
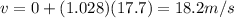
And the speed is just the magnitude of the velocity, so 18.2 m/s.