Answer:
a)
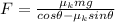
b)
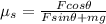
Step-by-step explanation:
In order to solve this problem we must first do a drawing of the situation and a free body diagram. (Check attached picture).
After a close look at the diagram and the problem we can see that the crate will have a constant velocity. This means there will be no acceleration to the crate so the sum of the forces must be equal to zero according to Newton's third law. So we can build a sum of forces in both x and y-direction. Let's start with the analysis of the forces in the y-direction:
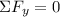
We can see there are three forces acting in the y-direction, the weight of the crate, the normal force and the force in the y-direction, so our sum of forces is:
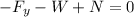
When solving for the normal force we get:
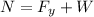
we know that
W=mg
and
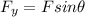
so after substituting we get that
N=F sin θ +mg
We also know that the kinetic friction is defined to be:
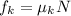
so we can find the kinetic friction by substituting for N, so we get:
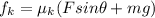
Now we can find the sum of forces in x:
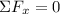
so after analyzing the diagram we can build our sum of forces to be:
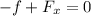
we know that:
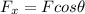
so we can substitute the equations we already have in the sum of forces on x so we get:
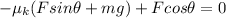
so now we can solve for the force, we start by distributing
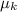 so we get:
so we get:
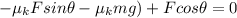
we add
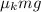 to both sides so we get:
to both sides so we get:
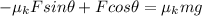
Nos we factor F so we get:
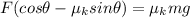
and now we divide both sides of the equation into
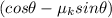 so we get:
so we get:
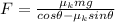
which is our answer to part a.
Now, for part b, we will have the exact same free body diagram, with the difference that the friction coefficient we will use for this part will be the static friction coefficient, so by following the same procedure we followed on the previous problem we get the equations:
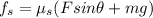
and
F cos θ = f
when substituting one into the other we get:
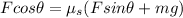
which can be solved for the static friction coefficient so we get:
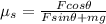
which is the answer to part b.