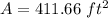For this case we have to:
If Sergio has 72 feet of fence then we have that the circumference of the fence (whose space is circular) is 72.
By definition, the circumference of a circle is given by:
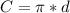
Where:
d: It is the diameter of the circumference
So:
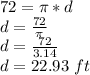
Then, the radius will be given by: r = 11.45 \ ft
Thus, the area of the circular portion will be:
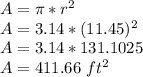
Thus, the area of the playing space is:
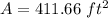
Answer: