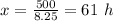Answer:
61 hours
Explanation:
See the attached figure to better understand the problem
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
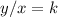 or
or
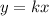
To find out the constant of proportionality k , divide the variable y (total earned) by the variable x (number of hours)
Kevin's wage
Take any point from the table
I take the point (2,16.50)
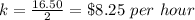
The equation of the proportional relationship is equal to
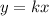
substitute the value of k
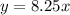
For y=$500.00
substitute the value of y in the equation and solve for x
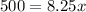
Divide by 8.25 both sides