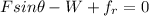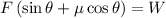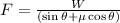Question

This force can either push the block upward at a constant velocity or allow it to slide downward at a constant velocity. The magnitude of the force is different in the two cases, while the directional angle θ is the same. Kinetic friction exists between the block and the wall, and the coefficient of kinetic friction is 0.340. The weight of the block is 51.0 N, and the directional angle for the force is θ = 44.0°. Determine the magnitude of when the block slides (a) up the wall and (b) down the wall.

Answer 1

Step-by-step explanation:

Given

coefficient of kinetic friction
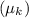`(\mu _k)`=0.34

inclination
`\theta =44`

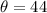
weight of block=51 N

(a) When block is moving upward friction force acts downward

thus

`Fsin\theta -W-f_r=0`

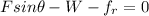
as block is moving with constant velocity thus
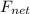`F_(net)` is zero

`f_r=\mu _kN=0.34* Fcos\theta`

`F\left ( \sin \theta -\mu \cos \theta \right )=W`

`F=(51)/(0.45)=113.31 N`

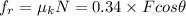
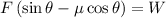
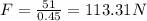
(b)When Block slides down the wall friction changes its direction to oppose the block

`Fsin\theta -W+f_r=0`

`F\left ( \sin \theta +\mu \cos \theta \right )=W`

`F=(W)/(\left ( \sin \theta +\mu \cos \theta \right ))`

`F=(51)/(0.939)=54.299 N`