Step-by-step explanation:
The given data is as follows.
Water flux,
 = 25
= 25
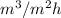
=
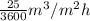
So, let velocity (u) =
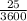 m/s =
m/s =
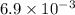
 = 998
= 998
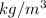
Pore size, d =
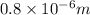
 = 0.9 cP =
= 0.9 cP =
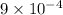 Pa.s
Pa.s
Hence, calculate the reynold number as follows.
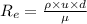
=
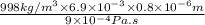
=
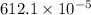
= 0.006
This means that the flow is laminar.
Now, we use Hagen-Poiseuille equation as follows.
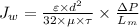
where,
 = membrane porosity = 0.35
= membrane porosity = 0.35
d =
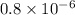 m
m
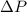 =
=
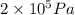
 =
=
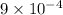
 = tortuosity
= tortuosity
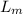 = membrane thickness =
= membrane thickness =
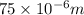
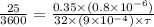
 = 3.73
= 3.73
Hence, the tortuosity factor of the pores is 3.73.
As flow resistance =
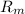
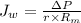
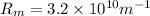
Water permeability is represented by
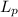 .
.
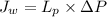
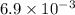 =
=
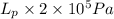

Therefore, the resistance to flow is
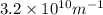 and its water permeability is
and its water permeability is
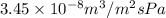 .
.