Answer:
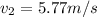
Step-by-step explanation:
We separate the problem in part 1 (speeding up the crate) and 2 (slowing down the crate). We take the direction the crates moves on at the beginning of the problem as the positive direction.
First we calculate the accelerations on each part using Newton's 2nd Law, which says F=ma. We will have:
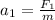
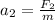
On part 1, the initial velocity is
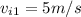 and
and
 is applied through a distance
is applied through a distance
 , so we calculate the final velocity with the formula
, so we calculate the final velocity with the formula
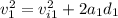 .
.
This
 will be the initial velocity of part 2, and we apply the same formula to calculate the final velocity
will be the initial velocity of part 2, and we apply the same formula to calculate the final velocity
 .
.
Substituting our accelerations:
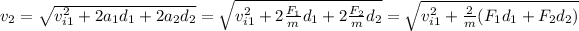
Which for our values is (noticing that
 must act in the negative direction, as said):
must act in the negative direction, as said):
