Question

The diagonals of a rhombus intersect at the point (0,4). If one endpoint of the longer diagonal is located at point (4,10), where is the other endpoint located?

Answer 1

The other endpoint is located at (-4,-2)

Explanation:

we know that

The diagonals of a rhombus bisect each other

That means-----> The diagonals of a rhombus intersect at the midpoint of each diagonal

so

The point (0,4) is the midpoint of the two diagonals

The formula to calculate the midpoint between two points is equal to

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

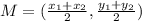
we have

`M=(0,4)`

`(x_1,y_1)=(4,10)`

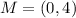
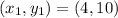
substitute

`(0,4)=((4+x_2)/(2),(10+y_2)/(2))`

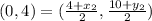
Find the x-coordinate
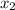`x_2` of the other endpoint

`0=(4+x_2)/(2)`

`x_2=-4`

Find the y-coordinate
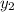`y_2` of the other endpoint

`4=(10+y_2)/(2)`

`8=10+y_2`

`y_2=-2`

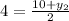
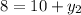
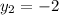
therefore

The other endpoint is located at (-4,-2)