Question

A virus that initially infected four people is spreading at a rate of 15% each week.

Answer 1

Answer: f(x) = 4(1.02)7x; spreads at a rate of approximately 2% daily

Step-by-step explanation: Use the formula y=P(1+r) ^x

Answer 2

"f(x) = 4(1.02)7x; spreads at a rate of approximately 2% daily"

Explanation:

Complete Question:

A virus that initially infected four people is spreading at a rate of 15% each week. The following function represents the weekly spread of the virus: f(x) = 4(1.15)x. Rewrite the function to show how quickly the virus spreads each day and calculate this rate as a percentage.

f(x) = 4(1.15)7x; spreads at a rate of approximately 1.5% daily

f(x) = 4(1.02)7x; spreads at a rate of approximately 2% daily

f(x) = 4(1.157)x; spreads at a rate of approximately 2.66% daily

f(x) = 4(1.02)x; spreads at a rate of approximately 0.2% daily

Solution:

The weekly number of people infected would be:

`f(x)=4(1.15)^x`

7 days in a week, so daily number of people infected would be:

`f(x)=4(1+r)^(7x)`

To find daily rate, we set these 2 equations equal and solve for r:

`4(1.15)^x=4(1+r)^(7x)\\1.15^x=(1+r)^(7x)\\1.15^x=((1+r)^7)^x\\1+r=1.02\\r=1-1.02=0.02`

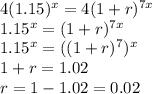
That is 0.02*100 = 2% daily

2nd answer choice is right.