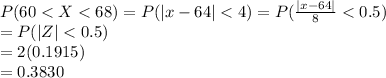Question

Suppose that X has a Poisson distribution with a mean of 64. Use normal approximation without applying continuity correction to approximate the following probabilities. Round your answers to 3 decimal places (e.g. 98.765). (a) Upper P left-parenthesis Upper X greater-than 80right-parenthesis equals (b) (c) Upper P left-parenthesis 60 less-than Upper X less-than-or-equal-to 68 right-parenthesis equals

Answer 1

Explanation:

Given that X has a Poisson distribution with a mean of 64.

We know in Poisson distribution mean = variance

Hence X will be normal after approximation as X is N(64,8)

Without continuity correction we find these by converting to Z score and using std normal distribution table.

a)
`P(X>80) = P(Z>(80-64)/(8) )\\=P(Z>2)\\=0.5-0.4772\\=0.0223`

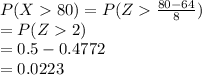
b)
`P(60<X<68) = P(|x-64|<4) = P((|x-64|)/(8) <0.5)\\=P(|Z|<0.5)\\= 2(0.1915)\\=0.3830`