Question

Find the length of a rectangular lot with a perimeter of 50 feet if the length is five feet more than the width.

Answer 1

The length of a rectangular lot is 15 feet

Explanation:

Let the width of rectangle be x

We are given that the length is five feet more than the width.

Length of rectangle = x+5

Perimeter of rectangle =
`2(l+b)=2(x+5+x)=2(2x+5)=4x+10`

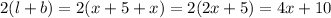
We are given that perimeter is 50 feet

So,
`4x+10=50`

`4x=40`

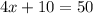
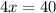
x=10

So, Length of rectangle = x+5=10+5=15

Hence the length of a rectangular lot is 15 feet

Answer 2

Width = 10 feet

Length = 15 feet

Explanation:

Let the width = x feet

Length = x + 5

Perimeter = 50 feet

2 * ( length + width) = 50

2 * (x+5 + x) = 50

2x + 5 = 50/2

2x + 5 = 25

2x = 25 - 5 = 20

x = 20/2 = 10

Width = 10 feet

Length = 10 + 5 = 15 feet