Question

Bank A pays 10% interest compounded annually on deposits, while Bank B pays 9% compounded daily. a. Based on the EAR (or EFF%), which bank should you use? You would choose Bank A because its EAR is higher. You would choose Bank B because its EAR is higher. You would choose Bank A because its nominal interest rate is higher. You would choose Bank B because its nominal interest rate is higher. You are indifferent between the banks and your decision will be based upon which one offers you a gift for opening an account.

Answer 1

Bank A should be chosen.

Step-by-step explanation:

Given:

Effective annual rate (EAR) of bank A = 10%

Bank B pays 9% compounded daily. EAR of bank B is calculated below:

EAR =
`( 1+(i)/(n))^(n) -1`

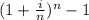
Where, i is 0.09

n is compounding period that is 365 (since it is compounded daily)

EAR =
`( 1+(0.09)/(365))^(365) -1`

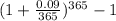
= 1.0942 - 1

= 0.0942 or 9.42%

Bank B pays EAR of 9.42%

Based on EAR, Bank A should be selected as it pays higher EAR of 10%.