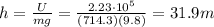Question

Calcular desde qué altura debe caer en punto muerto un automóvil de 7.000 N de peso para que adquiera la misma energía cinética que si marchase a 90 km/h

Answer 1

31.9 m

Step-by-step explanation:

First of all, let's start by calculating the mass of the object, which is given by

`m=(W)/(g)`

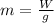
where

W = 7000 N is the weight

g = 9.8 m/s^2 is the acceleration of gravity

Substituting,

`m=(7000)/(9.8)=714.3 kg`

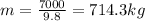
Now, we want this object to have the same energy as its kinetic energy when it travels at

`v=90 km/h = 25 m/s`

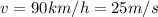
So when its kinetic energy is

`K=(1)/(2)mv^2 = (1)/(2)(714.3)(25)^2=2.23\cdot 10^5 J`

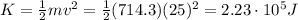
The gravitational potential energy is given by

`U=mgh`

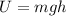
where h is the heigth of the object. We want the object to have the same energy as calculated for K, so we write

U = K

and solving for h, we find

`h=(U)/(mg)=(2.23\cdot 10^5)/((714.3)(9.8))=31.9 m`