Question

The Tampa Times polled 1,457 adults in the city to determine whether they put on their shirt before they put on their pants. Of the respondents, 48% said they put their shirt on first. Suppose 32% of all adults actually put their shirt on first. What are the mean and standard deviation of the sampling distribution? The mean is 0.48 and the standard deviation is 0.0131. The mean is 0.48 and the standard deviation is 0.0122. The mean is 0.48 and the standard deviation is 0.0182. The mean is 0.32 and the standard deviation is 0.0122. The mean is 0.32 and the standard deviation is 0.0131.

Answer 1

The mean is 0.32 and the standard deviation is 0.0122.

Explanation:

Given that the Tampa Times polled 1,457 adults in the city to determine whether they put on their shirt before they put on their pants.

Of the respondents, 48% said they put their shirt on first.

32% of all adults actually put their shirt on first

i.e. sample proportion is 48% while population proportion is 32%

Hence sampling distribution follows a distribution with mean = population proportion p

Hence here mean = 0.32

Std deviation of sampling distribution =
`\sqrt{(pq)/(n) } =\sqrt{(0.32(0.68))/(1457) } \\=0.0122`

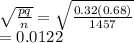
Hence option 3) The mean is 0.32 and the standard deviation is 0.0122.

is right