Question

A water tank in the shape of an inverted right circular cone that has a height of 12 ft and a base radius 6ft. If water is being pumped into the tank at a rate of 10 ft cubed per min , find the rate at which the water level is rising when the level of the water is 3 ft deep

Answer 1

`(dh)/(dt)=1.41\ ft/min`

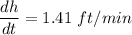
Step-by-step explanation:

Given that

h= 12 ft

r= 6 ft

h= 2 r

r=h/2

We know that volume of cone given as

`V=(1)/(3)\pi r^2h`

Now by putting the values

r=h/2

`V=(1)/(3)\pi\left((h)/(2)\right)^2h`

`V=(1)/(12)\pi h^3`

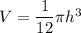
Given that when h= 3 ft

`(dV)/(dt)=10\ ft^3/min`

`V=(1)/(12)\pi h^3`

`(dV)/(dt)=(\pi)/(12)(3h^2)* (dh)/(dt)`

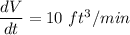
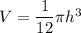
By putting the values

`10=(\pi)/(12)(3* 3^2)* (dh)/(dt)`

`(dh)/(dt)=1.41\ ft/min`

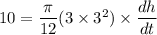
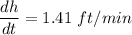
So the rate at which the water level is rising is 1.41 ft/min