Question

A father demonstrates projectile motion to his children by placing a pea on his fork's handle and rapidly depressing the curved tines, launching the pea to heights above the dining room table. Suppose the pea is launched at 7.39 m/s at an angle of 69.0° above the table. With what speed (in m/s) does the pea strike the ceiling 1.90 m above the table?

Answer 1

4.17 m/s

Step-by-step explanation:

To solve this problem, let's start by analyzing the vertical motion of the pea.

The initial vertical velocity of the pea is

`u_y = u sin \theta = (7.39)(sin 69.0^(\circ))=6.90 m/s`

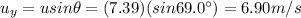
Now we can solve the problem by applying the suvat equation:

`v_y^2-u_y^2=2as`

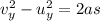
where

`v_y` is the vertical velocity when the pea hits the ceiling

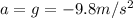`a=g=-9.8 m/s^2` is the acceleration of gravity

s = 1.90 is the distance from the ceiling

Solving for
`v_y`,

`v_y = √(u_y^2+2as)=√((6.90)^2+2(-9.8)(1.90))=3.22 m/s`

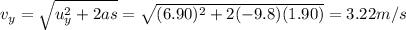
Instead, the horizontal velocity remains constant during the whole motion, and it is given by

`v_x = u cos \theta = (7.39)(cos 69.0^(\circ))=2.65 m/s`

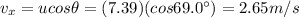
Therefore, the speed of the pea when it hits the ceiling is

`v=√(v_x^2+v_y^2)=√(2.65^2+3.22^2)=4.17 m/s`