Question

Triangle A has an area equal to one-third the area of Triangle B. Triangle A has an area of 3 1/2 square meters.

a. Gerard wrote the equation B/3 = 3 1/2. Explain what BB represents in the equation.
b. Determine the area of Triangle B.

Answer 1

Answers:

A. B 1/3 represents the area of triangle B

B. Triangle B area = 21/2 m² or 10 1/2 m² or 10.5 m²

Explanation:

Ok, we have two triangles measured in square meters (m²)

∆ a = 1/3 b and ∆ b = 3 1/2

Since these two areas have something in common (symbol a) we can consider they are almost the same, so we put them like this:

∆ a => 1/3 b = 3 1/2 <= ∆ b

Now that we know we can move some values. first we are gonna multiply the mixed fraction (3 1/2) to make it a regular fraction. As 3 is a whole, we can also write it on the following way:

`(3)/(1) +(1)/(2)`

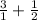
We add these fractions:

`(3)/(1) +(1)/(2) = ((3x2)+(1x1))/(1x2) =(6+1)/(2) =(7)/(2)`

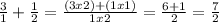
The equation with this part solved is:

`(1)/(3) b=(7)/(2)`

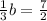
Since the 1/3 is multiplying, it goes to the other side dividing the number on the right:

`b=((7)/(2) )/((1)/(3) )`

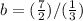
And then, we can solve the rest by inverting the second fraction (
`(1)/(3)`) and multiplying it by the first one:

`b=(7)/(2) / (1)/(3) \\`

`b=(7)/(2) x (3)/(1) =(7x3)/(2x1) =(21)/(2)`

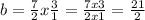
And that's it. Let me know if you have any doubts :D