Question

The product of two consecutive positive integers is 1332 explain how you can write and solve a quadratic equation to find the value of the larger integer

Answer 1

The product of two consecutive positive integers is 1332. The larger number is 37.

SOLUTION:

Given, the product of two consecutive positive integers is 1332.

Let the larger number be x.

Then the smaller number is x – 1 [as the given numbers are consecutive]

Product of the two numbers is 1332 → larger number
`*` smaller number = 1332

x(x – 1) = 1332

(x)x – (x)(1) = 1332

`\begin{array}{l}{x^(2)-x=1332} \\ {x^(2)-x-1332=0}\end{array}`

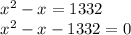
This is quadratic equation. let us find the x value by factorization method.

we need to make the two terms product as such that, difference of both numbers should be equal to 1, as x coefficient is 1.

`x^(2)-x-2 * 666=0`

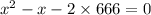
keep doing this until we get the difference equals to 1.

`x^(2)-x-4 * 333=0`

`\mathrm{x}^(2)-\mathrm{x}-12 * 111=0`

`x^(2)-x-36 * 37=0`

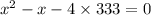
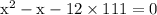
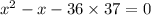
we got difference 1 that is 37 – 36 = 1

writing the x coefficient in terms of those numbers (36, 37)

`\mathrm{x}^(2)-(37-36) \mathrm{x}-36 * 37=0`

`x^(2)-37 x+36 x-36 * 37=0`

now, take the common terms

x(x – 37) + 36(x – 37) = 0

(x – 37)(x + 36) = 0

x – 37 = 0 or x + 36 = 0

x = 37 or -36

we can neglect -36, because given numbers are positive numbers.

Hence, the larger number is 37

Answer 2

The numbers can be written as x and x + 1. Set the product of the numbers equal to 1,332 to get x(x + 1) = 1,332. You can solve the quadratic equation by using the quadratic formula, completing the square, or factoring. When you solve the quadratic equation, you find that x = –37 and 36. Since the question asked for positive integers, the only viable solution is x = 36. To solve for the larger integer, you add 1 to 36 to get an answer of 37.