Answer:
The standard deviation of given probability distribution is 0.767.
Explanation:
We are given the following information in the question:
X: 0 1 2 3 4
P(x): 0.4521 0.3970 0.1307 0.0191 0.0010
Formula:
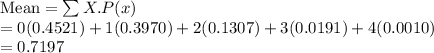
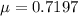
Formula:
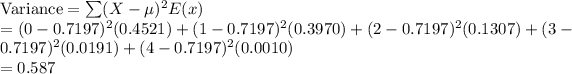
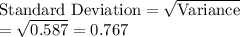
The standard deviation of given probability distribution is 0.767.