Question

The thin-walled cylindrical pressure vessel is subjected to an internal pressure of 15 MPa. The vessel is 3m long, has an inner radius of 0.5 m, and a thickness of 10 mm. It is constructed of structural A-36 steel. Compute the final diameter and the length of the pressure vessel.

Answer 1

Final diameter = 1.0032 m

Final length =3.0027 m

Step-by-step explanation:

Given that

P= 15 MPa

r= 0.5 m

L= 3 m

t=10 mm

For A-36 steel ,modulus of elasticity = 200 GPa

Hoop stress

`\sigma _h=(Pd)/(2t)`

`\sigma _h=(15* 1)/(2* 0.01)`

`\sigma _h=750 \ MPa`

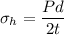
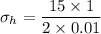
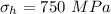
Longitudinal stress

`\sigma _l=(Pd)/(4t)`

`\sigma _l=(15* 1)/(4* 0.01)`

`\sigma _l=375 \ MPa`

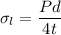
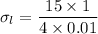
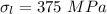
Hoop strain

`\varepsilon _h=(\sigma _h)/(E)-\mu (\sigma _l)/(E)`

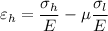
Take μ=0.26

`\varepsilon _h=(750)/(200* 1000)-0.26* (375)/(200* 1000)`

`\varepsilon _h=0.0032`

`\varepsilon _h=(\Delta d)/(d)`

`0.0032=(\Delta d)/(1)`

`\Delta d=0.0032`

`d_f=1+0.0032\ m`

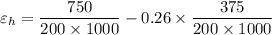
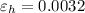
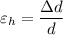
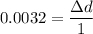
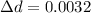
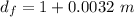
Final diameter = 1.0032 m

Longitudinal strain

`\varepsilon _l=(\sigma _l)/(E)-\mu (\sigma _h)/(E)`

`\varepsilon _l=(375)/(200* 1000)-0.26* (750)/(200* 1000)`

`\varepsilon _l=0.0009`

`\varepsilon _l=(\Delta L)/(L)`

`0.0009=(\Delta L)/(3)`

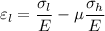
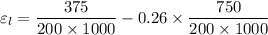
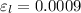
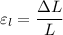
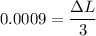
So the final length = 3.0027 m