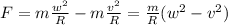Question

An engineer wants to design a circular racetrack of radius R such that cars of mass m can go around the track at speed without the aid of friction or other forces other than the perpendicular contact force from the track surface Find an expression for the required banking angle 0 of the 0 = track, measured from the horizontal. Express the answer in terms of m, R, , and g Suppose the race cars actually round the track at a speed F w > v. What additional radial force F, is required to keep the cars on the track at this speed? Express the answer in terms of m, R, U, w, and g.

Answer 1

1.
`tan \theta = (v^2)/(Rg)`

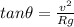
For the first part, we just need to write the equation of the forces along two perpendicular directions.

We have actually only two forces acting on the car, if we want it to go around the track without friction:

- The weight of the car, mg, downward

- The normal reaction of the track on the car, N, which is perpendicular to the track itself (see free-body diagram attached)

By resolving the normal reaction along the horizontal and vertical direction, we find the following equations:

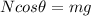`N cos \theta = mg` (1)

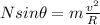`N sin \theta = m (v^2)/(R)` (2)

where in the second equation, the term
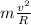`m(v^2)/(R)` represents the centripetal force, with v being the speed of the car and R the radius of the track.

Dividing eq.(2) by eq.(1), we get the following expression:

`tan \theta = (v^2)/(Rg)`

2.
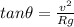
`F=(m)/(R)(w^2-v^2)`

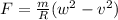
In this second situation, the cars moves around the track at a speed

`w>v`

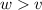
This means that the centripetal force term

`m(v^2)/(R)`

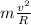
is now larger than before, and therefore, the horizontal component of the normal reaction,
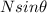`N sin \theta`, is no longer enough to keep the car in circular motion.

This means, therefore, that an additional radial force F is required to keep the car round the track in circular motion, and therefore the equation becomes

`N sin \theta + F = m(w^2)/(R)`

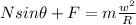
And re-arranging for F,

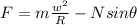`F=m(w^2)/(R)-N sin \theta` (3)

But from eq.(2) in the previous part we know that

`N sin \theta = m (v^2)/(R)`

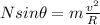
So, susbtituting into eq.(3),

`F=m(w^2)/(R)-m(v^2)/(R)=(m)/(R)(w^2-v^2)`