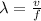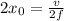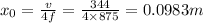Answer:0.0982 m
Step-by-step explanation:
Given
distance between two loudspeaker is 5 m
frequency (f )=875 Hz
speed of sound (v)=344 m/s
Let
 be the smallest distance moved by observer then
be the smallest distance moved by observer then
Position of observer w.r.t to first speaker is
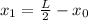
Position of observer w.r.t to second speaker is
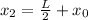

For Destructive interference
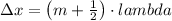
For minimum m=0
and