Answer:
a)
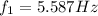
b)
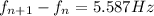
Step-by-step explanation:
The frequency of the
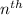 harmonic of a vibrating string of length L, linear density
harmonic of a vibrating string of length L, linear density
 under a tension T is given by the formula:
under a tension T is given by the formula:
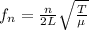
a) So for the fundamental mode (n=1) we have, substituting our values:
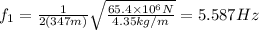
b) The frequency difference between successive modes is the fundamental frequency, since:
