Question

A person standing at the edge of a seaside cliff kicks a stone, horizontally over the edge with a velocity of 18 m/s. The cliff is 52 m above the waters surface

A. How long does it take for the stone to fall to the water
B. What is the vertical velocity component of the stone just before it hits the water
C. What is the horizontal velocity component of the stone just before it hits the water
D. What is the total velocity of the stone just before it hits the water ?

Answer 1

A) The time taken by the stone to reach the ground will be 3.257 Seconds

B) The Initial vertical velocity will be zero

C) The horizontal velocity doesn’t change, so it remains the same i.e., 18m/s.

D) The total velocity of the stone just before it hits the water is 36.645 m/s.

A)Explanation :

When the stone is kicked, there are two components act on the stone. One is in the horizontal direction, and the other in downward vertical direction.

Also Initial vertical component of velocity will be zero as the stone is kicked horizontally.

So, the time taken will be given by applying Newton’s Equation of Motion

Or, y=
`v_(i) t+(1)/(2) g t^(2)`

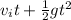
Where y = vertical downward distance

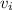`v_i`=initial vertical velocity=0 m/s

t = time taken to reach the ground

Substituting the values in the above equation, we find

-52 = 0 +
`(-9.8 * t^(2))/(2)`

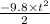
or,
`t^2`=
`(-52 * 2)/(-9.8)`

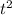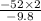
or, t =
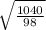`\sqrt{(1040)/(98)}` = 3.257 s

B) Explanation

The Initial vertical velocity will be zero as the stone is kicked horizontally

C)Explanation

The horizontal velocity component is not under the influence of gravity, so it remains the same, and moves constant velocity horizontally.

D) Explanation

We will firstly find the final vertical velocity using one of the equations of motion

`v_f`=
`\mathrm{v}_{\mathrm{i}}+\mathrm{at}^(2)`

Substituting the values in the above equation, we find

`v_f` =
`0-9.8 * 3.257`=-31.92 m/s

Now, Total Velocity (v) is given by

v =
`\sqrt{v_(x)^(2)+v_(y)^(2)}`

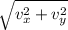
where,

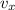`v_x`= Horizontal velocity

`v_y`= Vertical velocity

Substituting the values in the above equation, we find

v =
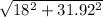`\sqrt{18^(2)+31.92^(2)}`= 36.645 m/s