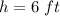Question

A bike ramp is in the shape of a right triangle. What is the height of the ramp?

Answer 1

Option C. 6 ft

Explanation:

Let

h ----> the height of the ramp

we know that

The ramp is in the shape of a right triangle

so

Applying the Pythagoras theorem

`c^(2)=a^(2)+b^(2)`

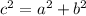
where

c is the hypotenuse of the right triangle (the greatest side)

a and b are the legs of the right triangle

substitute the given values

`10^(2)=h^(2)+8^(2)`

`100=h^(2)+64`

`h^(2)=100-64`

`h^(2)=36`

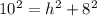
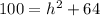
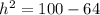
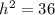
square root both sides

`h=6\ ft`