Question

A rectangle with vertices located at (−3, 4) and (5, 4) has an area of 32 square units. Determine the location of the other two vertices.

Answer 1

One possible answer: at (-3,0) and (5,0). The other possible answer (-3,8) and (5,8).

Explanation:

The first step in resolving coordinates problems is usually to plot them. The two given vertices are shown in the first image.

The other information given was the area enclosed by the rectangle. The area of a rectangle is its base multiplied by its height:
`A=b* h`

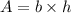
To find the location of the other two vertices it is necessary to recall a property of rectangles: all their internal angles are right angles, or equivalently, their sides are perpendicular. Given that two of their vertices are aligned with the cartesian grid -in which horizontal lines are perpendicular to vertical lines- the other vertices are located right above or below them... whether they are above or below it can't be determined by the information given, because there are two possible choices that satisfy the area condition.

The base of the rectangle is the distance between the two gives vertices, and it's found through the formula that measures the lenght between two points with coordinates
`(x_1,y_1)` and
`(x_2,y_2)`:
`d=√((x_2-x_1)^2+(y_2-y_1)^2)`.

In this case:
`b=√((5-(-3))^2+(4-4)^2)=√((5+3)^2+0^2)=√(64)=8`.

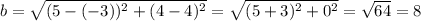Inserting the base into the area equation:
`32=8* h\quad\Rightarrow h=32/8=4`.

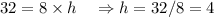The height of the resulting rectangle is 4 units, but it can be above the given points or below them. Thus, we arrive at the two possible answers shown in the images. One possible answer: at (-3,0) and (5,0). The other possible answer (-3,8) and (5,8).