Question

One side of a triangle is increasing at a rate of 5 cm/sec and a second side is increasing at a rate of 7 cm/sec. If the area of the triangle remains constant, at what rate does the angle between the sides change when the first side is 20 cm long, the second side is 50 cm long, and the angle is π 3 ?

Answer 1

The rate of angle is 26.25 rad/sec.

Step-by-step explanation:

Given that,

First side of triangle a= 20 cm

Second side of triangle b= 50 cm

One side of a triangle is increasing at a rate = 5 cm/sec

Second side is increasing at a rate = 7 cm/s

Angle
`\theta=(\pi)/(3)=60^(\circ)`

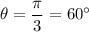
If the area of the triangle remains constant,

We need to calculate rate of angle

Using formula of area of triangle

`A=(1)/(2)ab\sin\theta`

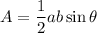
On differentiating

`(dA)/(dt)=(1)/(2)ab\cos\theta(d\theta)/(dt)+(1)/(2)a\sin\theta(db)/(dt)+(1)/(2)b\sin\theta(da)/(dt)`

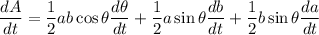
Put the value into the formula

`0=(1)/(2)*20*50\cos60(d\theta)/(dt)+(1)/(2)*20\sin60*7+(1)/(2)*50\sin60*5`

`(d\theta)/(dt)=(35√(3)*(25)/(2)√(3)*5)/(250)`

`(d\theta)/(dt)=26.25\ rad/sec`

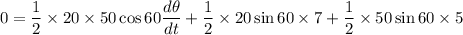
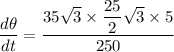
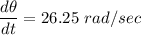
Hence, The rate of angle is 26.25 rad/sec.