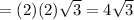Simplify - 2i √( - 12) Enter your answer in simplest radical form, in the box. ​

Question

Simplify


`- 2i √( - 12)`
Enter your answer in simplest radical form, in the box.
​

Answer 1

Answer:
`4√(3)`

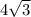
Explanation:

For this exercise it is important to remember the following:

`i=√(-1) \\\\i^2=-1`

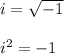
Given the following expression:

`-2i√(-12)`

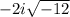
You can notice that the radicand (the number inside the square root) is negative. Therefore, in order to simplify the expression, you need to follow these steps:

1. Replace
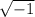`√(-1)` with
`i` and simplify:

`(-2i)(i)√(12)=-2i^2√(12)=-2(-1)√(12)=2√(12)`

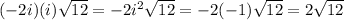
2. Descompose 12 into its prime factors:

`12=2*2*3=2^2*3`

3. Substitute into the expression:

`=2√(2^2*3)`

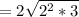
4. Since
`\sqrt[n]{a^n}=a`, you can simplify it:

`=(2)(2)√(3)=4√(3)`