Answer:
b) 49%
Step-by-step explanation:
To answer this question, we must assume that the population of gerbils is in Hardy-Weinberg equilibrium.
According to this law, the frequencies of the genotypes will be:
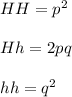
Where p is the frequency of the H allele and q is the frequency of the h allele.
p+q=1
If 18% of the population has short hair, the frequency of the hh genotype is 0.18.
Therefore:
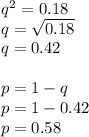
The expected Hh population is 2pq:
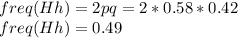
The percentage of the population expected to be heterozygous is 0.49x100=49%