Question

Ava is 400m west of the restaurant, walking east at 2.15m/s. Barney is 300m east of the restaurant. He begins walking west at 2.75m/s 4 seconds after Ava begins walking. If both of them keep walking until they meet, how far away from the restaurant will they meet? How long will it take them to get there?

Answer 1

They meet each other at a distance of 85.71 m far from the restaurant. Both A and B takes 39.86 seconds and 31.16 seconds respectively to reach the restaurant after they meet each other.

Explanation:

The relationship between speed, time and distance is
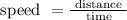`\text { speed }=\frac{\text { distance }}{\text { time }}` To find how far away from the restaurant will they meet, calculate the time taken to meet each other.
`time}=\frac{\text {total distance}}{\text {relative speed }}`

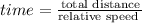
Total distance between A and B = 700 m and relative speed when travelling in opposite direction = speed of A + speed of B = 2.15+2.75 = 4.9 m⁄s.
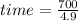`ti m e=(700)/(4.9)` = 142.85 seconds.

A and B are far from restaurant is known by subtracting the distance covered by A and B in 142.85 seconds. By using the formula speed= distance/time That is distance travelled by A in 142.85 seconds is 307.12 m and the distance travelled by B in 142.85 seconds is 392.83 m. Distance between restaurant and persons A and B = 392.83 – 307.12 = 85.71 m. Time taken by A to reach restaurant is 39.86 seconds and time taken by B to reach restaurant is 31.16 seconds.