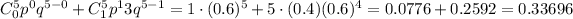Answer:
A. 0.2304
B. 0.98976
C. 0.91296
D. 0.33696
Explanation:
Forty percent of prison inmates were unemployed when they entered prison, then

Find all needed probabilities:
A. Exactly 3 were unemployed
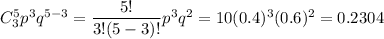
B. At most 4 were unemployed
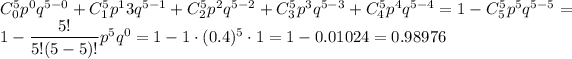
C. At least 3 were unemployed
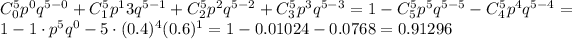
D. Fewer than 2 were unemployed