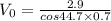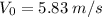Answer:
5.83 m/s
Step-by-step explanation:
This is a projectile motion problem.
Let's call
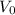 the initial velocity
the initial velocity
In x-coordinate:
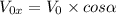
where α is 44.7°
In y-coordinate:

In x-coordinate the displacement is:
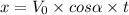
where t is time. Isolating the initial speed and replacing with x = 2.9 (the distance travelled in x direction) :
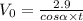
In y-coordinate the displacement is:

Replacing with the initial velocity, y = 0.436, alpha = 44.7° and g = 9.81:
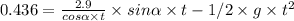
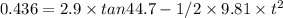
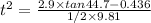
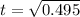
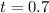
Replacing this value in the previous initial velocity equation: