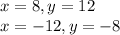Question

One integer is 4 less than another. The sum of their squares is 208. Find the integers

Answer 1

x=8, y=12

x=-12, y=-8

Explanation:

Let's set some variables.

`x` and
`y` will be our two numbers.

Since they're integers, we don't have to deal with decimals. This makes things significantly easier for us.

Let's now rephrase your question into equations using the integers:

`x=y-4\\x^2+y^2=208`

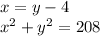
Now let's substitute:

`(y-4)^2+y^2=208\\\\y^2-8y+16+y^2=208\\\\2y^2-8y+16-208=0\\\\2y^2-8y-192=0`

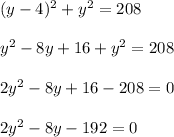
We can use the quadratic formula to find out the value of
`y`:

`y=(-b+√(b^2-4*a*c) )/(2*a)` or
`y=(-b-√(b^2-4*a*c) )/(2*a)`

`ay^2+by+c=0\\\\a=2, b=-8,c=-192\\\\y=(-(-8)+√((-8)^2-4*(2)*(-192)))/(2*(2))\\y=(-(-8)-√((-8)^2-4*(2)*(-192)))/(2*(2))\\\\y=(8+√(64+1536))/(4)\\y=(8-√((64+1536))/(4)\\\\y=(8+√(1600))/(4)\\y=(8-√((1600))/(4)\\\\y=(8+40)/(4)\\y=(8-40)/(4)\\\\y=(48)/(4)\\y=(-32)/(4)\\\\y=12\\y=-8\\`

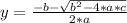
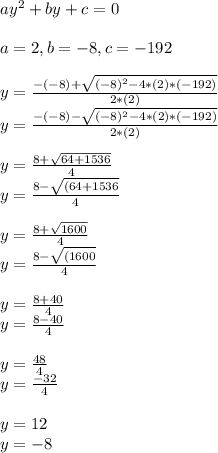
Now, substitute the value back into the equation for
`x`:

`x=(12)-4\\x=(-8)-4\\\\x=8\\x=-12\\`

Let's check the values with the second part of the question:

`x^2+y^2=208\\\\(8)^2+(12)^2=64+144=208\\(-12)^2+(-8)^2=144+64=208\\`

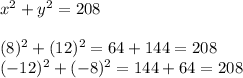
So, you have two possible solutions:

`x=8,y=12\\x=-12,y=-8`