Answer:
The integers are 32 and 28 .
Solution:
Let the two integers be x and y.
It is given that sum of two integers is 60. Writing it in equation form we get,
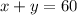 ……………..(Let this be equation 1)
……………..(Let this be equation 1)
Again it is given that, the difference between the two integers is 4. Writing it in equation form we get,
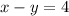 ………………….(let this be equation 2)
………………….(let this be equation 2)
Adding Equation 1 and equation 2 we get,
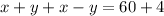
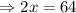
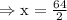
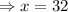
Substituting the value of x = 32 in equation 2 we get


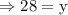
Therefore, the two integers are 32 and 28.