Question

alicias average speed riding her bike is 11.5 miles her hour. she takes a round trip of 40 miles. it takes her 1 hour and 20 minutes with the wind and 2 hours and 30 minutes against the wind. write an expression for alicias time with the wind

Answer 1

The speed of the wind is 3.5 miles per hour.

Solution:

Let x be the speed of the wind

The total time of the trip =
`(20)/(11.5+x)+(20)/(11.5-x)`

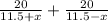
From the Question we know the total time = 1 hr 20 minutes +2 hrs 30 minutes = 3 hrs 50 minutes.

We transform the time in hours and solve the equation:

`3 \text { hrs } 50 \text { minutes }=3+(50)/(60)=3+(5)/(6)=(23)/(6)`

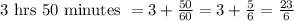
The equation needed to solve the problem is:

`\begin{array}{l}{(20)/(11.5+x)+(20)/(11.5-x)=(23)/(6)} \\\\ {6 * 20(11.5-\mathrm{x})+6 * 20(11.5+\mathrm{x})=23(11.5-\mathrm{x})(11.5+\mathrm{x})} \\\\ {1350-120 \mathrm{x}+1380+120 \mathrm{x}=23\left(132.25-\mathrm{x}^(2)\right)}\end{array}`

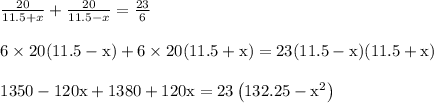
Evaluate to find the value of x.

`\begin{array}{l}{2760=3041.75-23 x^(2)} \\\\ {23 x^(2)=281.75} \\\\ {x^(2)=(281.75)/(23)} \\\\ {x^(2)=12.25} \\\\ {\text {Taking square root. }} \\ {x=\pm 3.5} \\ {x_(1)=-3.5} \\ {x_(2)=3.5}\end{array}`

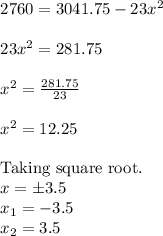
The speed of wind in positive number so the solution is x = 3.5 miles per hours.