Answer:
The time taken by the bar to reach the bottom t=4.886s
Given:
Displacement of the bar S=9.2m
Angle of inclination
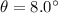
Coefficient of friction factor
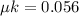
To find:
How long it takes to reach the bottom ‘t’
Step by Step Explanation:
Solution:
We know that the formula for weight of the soap bar is given as
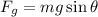
The frictional force acting on this soap bar is determined by
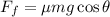
To determine the constant acceleration of the bar, we derive as
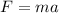
Here
 and thus
and thus
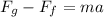
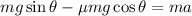
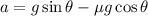
Where
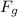 =Force imparted due to weight
=Force imparted due to weight
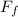 =Frictional Force
=Frictional Force
m=Mass of the bar
g=Acceleration due to gravity
a=Acceleration of the bar
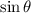 and
and
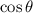 are the angles involved in the system
are the angles involved in the system
If the bar starts from the rest
Equations of motion involved in calculating the displacement of the bar is given as
 , From this
, From this
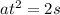


Where s= displacement or length moved by the bar
a=Acceleration of the bar
t=Time taken to reach bottom
Substitute all the known values in the above equation we get
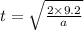 and we know that
and we know that
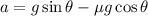

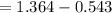
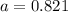
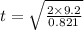
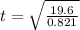
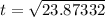
t=4.886s
Result:
Thus the time taken by the bar to reach the bottom is t=4.886s