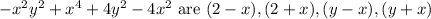ANSWER:
The factors of
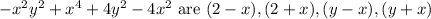
SOLUTION:
Given, polynomial is
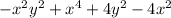
This is an polynomial in two variables with degree 4
So the given polynomial will have 4 factors.
We need to factorise the given polynomial.
Now,
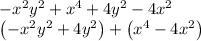
[writing terms with y as one part and remaining as another part]\
Taking the common terms out of brackets.
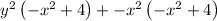
Taking
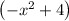 as common
as common
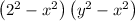
![(2-x)(2+x)(y-x)(y+x)\left[a^(2)-b^(2)=(a-b)(a+b)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ekh6ozmavwvjyxbo41u9940kgnb0zlv97k.png)
Hence the factors of