Answer:
The value of h must be greater than or equal to 8 inches
The minimum value of h is 8 inches
Explanation:
Let
h ----> the possible heights (in inches) of the triangle
we know that
The area of triangle is equal to

where
b is the base length
h is the height
In this problem we have

Remember that the word "at least" means "greater than or equal to"
so
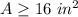
The inequality that represent this problem is
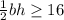
substitute the value of b
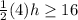
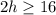
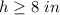
The value of h must be greater than or equal to 8 inches
The minimum value of h is 8 inches