Question

Problem

Find the slope and y-intercept of the line that is \green{\text{perpendicular}}perpendicularstart color #28ae7b, start text, p, e, r, p, e, n, d, i, c, u, l, a, r, end text, end color #28ae7b to \blue{y = -\dfrac{2}{3} x + 5}y=−32​x+5start color #6495ed, y, equals, minus, start fraction, 2, divided by, 3, end fraction, x, plus, 5, end color #6495edand passes through the point \red{(-6, -4)}(−6,−4)​

Answer 1

pls type properly -_-

Explanation:

Answer 2

The slope is 3/2 and y-intercept is 5.

Explanation:

_______________________________________

The question states:

Find the slope and y-intercept of the line that is perpendicular to

`y=-(2)/(3)x+5`

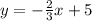
and passes through the point (-6, -4)

_______________________________________

From functions, we know that if two lines, called line 1 and line 2, are perpendicular, then it is true that:

`m_(1)* m_(2)=-1 \\ \\ \\ Where: \\ \\ m_(1): Slope \ of \ line \ 1 \\ \\ m_(2): Slope \ of \ line \ 2`

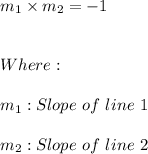
If the given line is called line 1, then:

`m_(1)=-(2)/(3)`

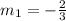
Then:

`m_(2)=-(1)/(m_(1)) \\ \\ m_(2)=-(1)/(-(2)/(3)) \\ \\ \boxed{m_(2)=(3)/(2)}`

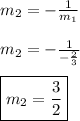
On the other hand, the y-intercept can be found as:

`y=m_(2)x+b \\ \\ y=(3)/(2)x+b \\ \\ For \ (x,y)=(-6,-4) \\ \\ -4=(3)/(2)(-6)+b \\ \\ Solving \ for \ b: \\ \\ -4=-9+b \\ \\ b=9-4 \\ \\ \boxed{b=5}`

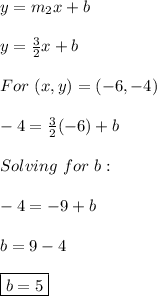
Find the slope is 3/2 and y-intercept is 5.