Question

011 10.0 points

To win the game, a place kicker must kick a
football from a point 52 m (56.8672 yd) from
the goal, and the ball must clear the crossbar,
which is 3.05 m high. When kicked, the ball
leaves the ground with a speed of 25 m/s at
an angle of 35.9° from the horizontal.
The acceleration of gravity is 9.8 m/s.
By how much vertical distance does the ball
clear the crossbar?
Answer in units of m.

I’m really confused please help me understand these steps for my quiz!

Answer 1

2.47 m

Step-by-step explanation:

Let's calculate first the time it takes for the ball to cover the horizontal distance that separates the starting point from the crossbar of d = 52 m.

The horizontal velocity of the ball is constant:

`v_x = v cos \theta = (25)(cos 35.9^(\circ))=20.3 m/s`

and the time taken to cover the horizontal distance d is

`t=(d)/(v_x)=(52)/(20.3)=2.56 s`

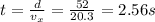
So this is the time the ball takes to reach the horizontal position of the crossbar.

The vertical position of the ball at time t is given by

`y=u_y t - (1)/(2)gt^2`

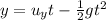
where

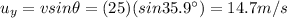`u_y = v sin \theta =(25)(sin 35.9^(\circ))=14.7 m/s` is the initial vertical velocity

g = 9.8 m/s^2 is the acceleration of gravity

And substituting t = 2.56 s, we find the vertical position of the ball when it is above the crossbar:

`y=(14.7)(2.56) - (1)/(2)(9.8)(2.56)^2=5.52 m`

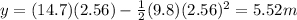
The height of the crossbar is h = 3.05 m, so the ball passes

`h' = 5.52- 3.05 = 2.47 m`

above the crossbar.