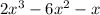Question

Let f(x) = 16x5 − 48x4 − 8x3 and g(x) = 8x2. Find f of x over g of x.

2x2 + 6x + 1
2x2 − 6x − 1
2x3 + 6x2 + x
2x3 − 6x2 − x

Answer 1

`2x^3-6x^2-x`

Explanation:

`(f(x))/(g(x))=(16x^5-48x^4-8x^3)/(8x^2)`

`(f(x))/(g(x))=(16x^5)/(8x^2)-(48x^4)/(8x^2)-(8x^3)/(8x^2)`

`(f(x))/(g(x))=(16)/(8)x^(5-2)-(48)/(8)x^(4-2)-(8)/(8)x^(3-2)`

`(f(x))/(g(x))=2x^(3)-6x^2-1x^1`

`(f(x))/(g(x))=2x^3-6x^2-x`

Answer 2

First, we have to express the fraction between these two functions:

`(f(x))/(g(x))=(16x^(5)-48x^(4)-8x^(3))/(8x^(2) )`

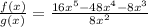
Then, we separate the denominator to operate each term in the numerator:

`(16x^(5))/(8x^(2))-(48x^(4))/(8x^(2))-(8x^(3))/(8x^(2))`

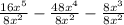
Now, we have to divide numbers and terms, remember that power dividing requires to subtract exponents and maintain the same base:

`2x^(3)-6x^(2)-x`

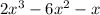
Therefore, the result of this function division is:

`2x^(3)-6x^(2)-x`