Question

29. Donut Delights, Inc. has determined that when x donuts are made daily, the profit P, in

dollars, is given by
P(x) = -0.001 x2 + 1.9x - 350
(a) What is the company's profit if 400 donuts are made daily?
(b) How many donuts should be made daily in order to maximize the company's profit? Show
work.

Answer 1

(a) When 400 donuts are made daily the company's profits is 250 dollars.

(b) The Company should produce 950 donuts daily in order to maximize its profits.

Explanation:

Profit function P(x) = - 0.001 x² + 1.9x - 350

where p is the profit and x is the quantity of donuts made daily.

(a) If x = 400, the company's profit is:

P(x) = - 0.001 x² + 1.9x - 350

= - 0.001 (400)² + 1.9(400) - 350

=
`-(160000)/(1000) + (7600)/(10) - 350`

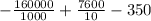
= - 160 + 760 - 350

= 760 - 510

= 250

(b) The profit of a firm is maximum when MR = MC or MR - MC = 0 which is also known as break even point. In other words, at break-even point the profit function equals to zero. ∴,

`(d)/(dx) P(x) = (d)/(dx)(- 0.001x^(2) + 1.9x - 350)`

`(d)/(dx)(- 0.001x^(2) + 1.9x - 350) = 0`

`- 0.002 x + 1.9 = 0`

`x = (1.9)/(0.002)`

`x = 950`

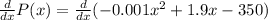
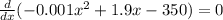
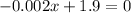
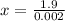
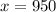
Therefore, the Company should produce 950 donuts daily in order to maximize its profits.