Answer:
No solution:
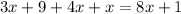
One solution:
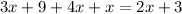
Infinitely many solution:

Explanation:
The given equation is
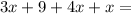
It can be written as
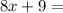
Here slope is 8 and y-intercept is 9.
No solution: For all values of x, LHS≠RHS. It means the lines have same slope but different y-intercept.
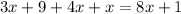
One solution: For unique value of x, LHS=RHS. It means the lines have different slopes.
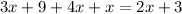
Infinitely many solution: For all values of x, LHS=RHS. It means the lines have same slope and y-intercept.

Note: There are more possible equations for no solutions and one solution.