Question

A certain sum quadruples in 3 years at compound interest, interest being compounded annually. In how many years will it become 64 time itself?

Answer 1

In 9 years, amount becomes 64 times of itself.

SOLUTION:

Given, a certain sum quadruples in 3 years at compound interest, interest being compounded annually.

We know that, When interest is compound annually:

`\text { Amount }=P\left(1+(R)/(100)\right)^(n)`

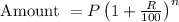
Given that,

Principal = Rs.100%

Amount = Rs.400

Rate = r%

Time = 3 years

By substituting the values in above formula, we get,

`400=100 *\left[1+\left((R)/(100)\right)\right]^(3)`

`4=1\left[1+\left((R)/(100)\right)\right]}^(3)` --- eqn 1

If sum become 64 times in the time n years then,

`64=\left(1+\left((R)/(100)\right)\right)^n`

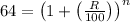
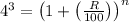`4^(3)=\left(1+\left((R)/(100)\right)\right)^(n)` --- eqn 2

Using equation (1) in (2), we get

`\begin{array}{c}{\left(\left[1+\left((R)/(100)\right)\right]^(3)=\left(1+\left((R)/(100)\right)\right)^(2)\right.} \\ {\left[1+\left((R)/(100)\right)\right]^(9)=\left(1+\left((R)/(100)\right)\right)^(n)}\end{array}`

Thus, n = 9 years by comparing on both sides.

Hence, in 9 years, amount becomes 64 times of itself.