Answer:
Explicit form:
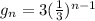
Recursive form:
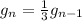 with
with
 .
.
Explanation:
The first term is 3 and we are dividing by 3 each time.
Another way to say we are dividing by 3 each time is to say we are multiplying by factors of 1/3.
If the first term is
 and
and
 is the common ratio then the geometric sequence in explicit form is:
is the common ratio then the geometric sequence in explicit form is:
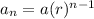
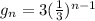
The recursive form for a geometric sequence is
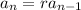 with
with
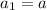 where
where
 is the common ratio and
is the common ratio and
 is the first term.
is the first term.
So the recursive form for our sequence is
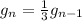 with
with
 .
.