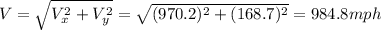Answer:
984.8 mph
Step-by-step explanation:
The initial velocity of the jet in terms of components is
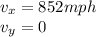
where we took east as positive x-direction and north as positive y-direction.
The velocity of the wind is
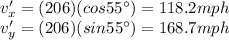
So, the resultant velocity of the jet considering also the wind is

And so the new speed of the jet is