Question

What are the next three terms of the geometric sequence below?
875, 175, 35, 7, ...

Answer 1

1.4, 0.28, 0.056

Explanation:

Each number is divided by 5

(875/5=175 175/5=35)

Answer 2

The next three terms of the geometric sequence are 875, 175, 35, 7 is 1.4, 2.8, and 0.56.

Solution:

Given Geometric sequence is 875, 175, 35, 7.

We need to find the next three sequence.

A geometric sequence is one where any value in the sequence can be determined using the formula:

`\boldsymbol{a}_{\mathbf{n}=\mathbf{a}_(1)(\mathbf{r})^(n-1)}`

Where

n is the nth term in the sequence,
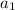`a_(1)` is the first term (in this case, 875) and "r" is the rate of change between them.

To find r, you simply divide the second term by the first:

`(175)/(875) = 0.2`

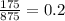
Inserting
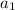`a_(1)` = 875 and r=0.2 into the formula above, you have the equation for the sequence:

`a_(5)=875 *(0.2)^(n-1)`

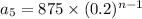
To find 5th sequence:

`a_(5=875 *(0.2)^(5-1))=875 *(0.2)^(4)=875 * 0.0016=1.4`

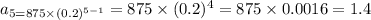
To Find 6th Sequence:

`a_(5=875 *(0.2)^(6-1))=875 *(0.2)^(5)=875 * 0.0032=0.28`

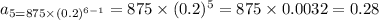
To Find 7th Sequence:

`a_(5)=875 *(0.2)^(7-1)=875 *(0.2)^(6)=875 * 0.000064=0.056`

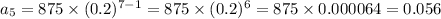
Hence the next three terms of the geometric sequence are 875, 175, 35, 7, 1.4, 0.28, and 0.056.